Историческая справка: английский физик-метролог Кэтер (Henry Kater) первым изготовил в 1817г оборотный маятник и нашел ему практическое применение.

В экспозиции Музея СПб АППО находятся несколько физических приборов, созданных во второй половине XIX века: прибор для объяснения закона равных давлений, бароскоп, электрическая машина системы Рамедена, разрежающий насос с двумя цилиндрами.

Рисунок 1. Оборотный маятник на штативе

В их число входит реверсивный (оборотный) маятник с тремя чечевицами (рис. 1); изготовлен в мастерских фирмы «Лейбольда наследники», г. Кельн на Рейне, Германия.
Для понимания устройства и принципа действия простого оборотного маятника рекомендуем посмотреть видео, созданное специалистами МИФИ.
Оборотный маятник – один из множества физических приборов, предназначенных для определения ускорения свободного падения g.
Маятник из Музея СПб АППО состоит из стальной полосы шириной 2 см и толщиной 1 см. По всей длине полосы (150 см) нанесены сантиметровые деления. Маятник снабжен двумя осями вращения–призмами, которые обращены друг к другу острыми ребрами. Расстояние между призмами фиксированное 100 см. На полосу насажены три свинцовых груза в форме чечевиц; один груз можно перемещать между призмами, два другие можно снимать (рис. 2). Массы чечевиц связаны следующим соотношением:

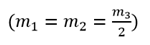
Маятник подвешивается на устойчивый деревянный штатив высотой 150 см (рис.3).
В видеофрагменте «Физический маятник» показано, что расстояние между центром качания маятника и осью вращения равно длине математического маятника и оба маятника имеют одинаковый период малых колебаний. Именно это свойство является принципом действия физического прибора, предназначенного для более точного по сравнению с математическим маятником измерения g.


Для экономии времени в видеофайле не показан процесс подготовки оборотного маятника с двумя чечевицами для измерения g: вначале с помощью метронома измеряют период колебаний маятника на одной призме, затем маятник переворачивают и определяют период колебаний на другой призме. Затем грузы равной массы перемещают так, чтобы период колебаний Т на каждой призме был одинаковым. Только при таком условии расстояние между осями-призмами будет приведенной длиной l, что позволяет использовать формулу периода колебаний математического маятника для косвенного измерения ускорения свободного падения в данном месте Земли:
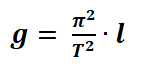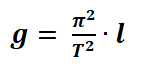^[1]
(Из учебника физики К.Краевича,1880.)

Рисунок 2. Подвижные свинцовые грузы с конусообразным отверстием в центре, чтобы видеть деления шкалы.	Рисунок 3.Крепление на штативе для подвеса маятника

---